You are here: Home >> Beginner’s Guide >> Other Topics >> Hedging with Betfair
This section outlines hedging strategies using Betfair. Hedging involves backing and laying the same selection after the odds have shifted in your favour. While the discussion below is specific to Betfair, the theory holds for any betting exchange that enables you to bet both for and against selections. Be sure to check out our online hedging calculator to play around with some numbers after you have read this guide.
Back and lay betting
A back wager is a wager that pays out if the selection wins, while a lay wager pays out if the selection doesn’t win. When you back an outcome you are playing the role of a traditional punter. When you lay an outcome you are playing the role of the bookmaker. This section presumes you are already familiar with backing and laying outcomes. To learn more about these terms, check out our guide on bookmakers vs. betting exchanges.
Arbitrage vs. hedging
Arbitrage and hedging differ in terms of timing. For our purposes, in a sports betting context, we define an arbitrage strategy as one that makes two or more simultaneous wagers on an event such that the net profit across those wagers is equal to or greater than $0.00 regardless of the event outcome.
In contrast, we define a hedging strategy as one that makes one or more wagers on an event that we have previously wagered on such that the net profit across the original and new wagers is equal to or greater than $0.00 regardless of the event outcome.
Arbitrage betting typically involves odds discrepancies between bookmakers, although opportunities occasionally arise due to bookmaker error. Hedging involves changes in odds over time, and can be achieved using the same bookmaker.
Hedging is more convenient with an exchange such as Betfair than it is with a traditional bookmaker. Suppose you have backed Tiger Woods to win a golf tournament and after the first day he leads the field. To hedge with a traditional bookmaker you would have to place wagers on the rest of the field while with Betfair you can simply place a lay wager on Tiger Woods.
Notation
The theory below uses the following notation. All betting wagers contain two variables:
1. The wager stake amount, which is a currency value ($, £, €, etc.)
2. The wager odds
The equations here use the decimal odds system which is popular in Australia, New Zealand and Europe. A winning $10 wager at decimal odds of 1.50 would return a $15 payout for a $5 profit. Decimal odds of 1.50 equate to 1/2 in fractional odds and -200 in American odds.
Hedging with Betfair requires at least two wagers. One wager will back the selection and the second will lay that selection. Let:
WB = back wager stake amount (i.e. $10.00)
DB = back wager decimal odds (i.e. 1.50)
WL = lay wager stake amount (i.e. $10.00)
DL = lay wager decimal odds (i.e. 1.45)
We have the opportunity to hedge for a guaranteed profit providing DB > DL. This is because the payout for a winning back wager will exceed the odds at which the losing lay wager has to pay out.
All references to * in the equations below denote the multiplication sign (i.e. 5 * 2 = 10). For order of operations, multiplication and division take precedent over addition and subtraction (i.e. 1 + 2 * 3 = 1 + (2 * 3) = 7). Figures in parentheses denote equation numbers (e.g. (1)). These are used to refer back to the formulas in the worked examples.
Note that for convenience we are ignoring the minimum stake amount ($5.00 for AUD accounts) as well as currency rounding.
Hedge betting
Our back and lay wagers will be on the same selection, e.g. the USA to win the men’s basketball Olympic Gold Medal. In this example the market is the ‘Olympic Gold Medal Winner for men’s basketball’ and the selection is ‘Team USA’. The Betfair odds on other selections (Spain, France, etc.) do not come into the hedging equations.
Any given hedge will both back and lay the selection. The table below shows the back and lay profits if the selection does or doesn’t win. Recall that the back wager is a winning bet if the selection wins, while the lay wager is a winning bet if the selection doesn’t win, and vice versa. The expressions in the table have been colour coded blue and red to denote profit (blue) and loss (red), before commissions.
| Profit if Selection Wins | Profit if Selection Loses | |
|---|---|---|
| Back wager | WB(DB – 1) | -WB |
| Lay wager | -WL* (DL – 1) | WL |
| Combined back and lay wagers | WB* (DB – 1) – WL* (DL – 1) | WL – WB |
There is no single hedging strategy when an opportunity arises. If you back an outcome and the lay odds become shorter than your original back odds, then you have a spectrum of options. Essentially, you can hedge your bets in three different ways.
1. Make a profit if the selection wins, with no profit or loss if it loses
2. Make a profit if the selection loses, with no profit or loss if it wins
3. Make a profit regardless of whether the selection wins or loses
The third strategy simply refers to every hedging strategy in-between (1) and (2). It consists of a spectrum of strategies where at least some money is won, regardless of the event outcome.
In the discussion below we will look at two basic hedging strategies. The first strategy, which we will call ‘unbiased hedging’, falls into category (3) above. This strategy will deliver the exact same profit, regardless of the event outcome. The second strategy, which we will call ‘biased hedging’, covers (1) and (2) above. A biased hedge provides a greater profit than an unbiased hedge if your predicted event outcome is correct, however a biased hedge will return no profit if you get it wrong. We employ a biased hedge when we have a strong opinion on the event outcome and an unbiased hedge when we have no strong opinion either way.
Obviously, every hedging strategy in-between a biased hedge and an unbiased hedge is possible, but for simplicity we will focus on just these two.
Unbiased hedging
With an unbiased hedge, the net profit if the selection wins will equal the net profit if the selection loses. Using our profit table above this can be expressed as:
Profit if selection wins = profit if selection loses
WB* (DB – 1) – WL* (DL – 1) = WL – WB
This can be rearranged and simplified to:
WB* (DB – 1) + WB = WL + WL* (DL – 1)
WB* DB – WB + WB = WL + WL* DL – WL
WB* DB = WL *DL
If we had initially made a back wager of amount WB at decimal odds DB and are looking to hedge because the lay odds (DL) are now less than DB, then we need to calculate the lay amount, WL. To do this we solve the equation above for WL.
WB* DB = WL* DL
WL = WB* (DB / DL) (1)
If we lay WL on the selection we will make the same profit regardless of the event outcome.
Now suppose we had initially made a lay wager of amount WL at decimal odds DL and are looking to hedge because the back odds (DB) are now greater than DL. We will hedge by making a back wager so we need to calculate the back amount, WB. To do this we solve the earlier equation for WB.
WB* DB = WL* DL
WB = WL* (DL / DB) (2)
If we back WB on the selection we will make the same profit regardless of the event outcome.
Biased hedging
With a biased hedge, we have a strong opinion on whether the back or lay wager is more likely to win. This strategy provides a greater profit if your prediction is correct, with no profit (as opposed so some profit) if you are wrong.
Strategy to profit if selection wins
We employ this strategy if we believe the back bet is most likely to win. The strategy will provide no profit or loss if the selection loses, but provides a greater profit than the unbiased strategy if the selection does win. We calculate our optimal hedge bet by setting our net profit/loss if the selection loses to zero (see earlier table).
WL – WB = 0
This can be rearranged to:
WL = WB (3)
Hence, if we had initially made a back wager of amount WB and wish to hedge our losses if the selection loses, we lay amount WL (which is equal to WB) at decimal odds DL.
Alternatively, if we had initially made a lay wager of amount WL and wish to hedge our losses if the selection wins, we can back amount WB (which is equal to WL) at decimal odds DB.
Strategy to profit if selection loses
We employ this strategy if we believe the back bet unlikely to win. The strategy will provide no profit or loss if the selection wins, but provides a greater profit than the unbiased strategy if the selection loses. We calculate our optimal hedge bet by setting our net profit/loss if the selection wins to zero (see earlier table).
WB* (DB – 1) – WL* (DL – 1) = 0
This can be rearranged to:
WB* (DB – 1) = WL* (DL – 1)
If we had initially made a back wager of amount WB we need to solve for WL to make our lay wager.
WL = WB* (DB – 1) / (DL – 1) (4)
Conversely, if we had initially made a lay wager of amount WL we need to solve for WB to make our back wager.
WB = WL* (DL – 1) / (DB – 1) (5)
Worked examples
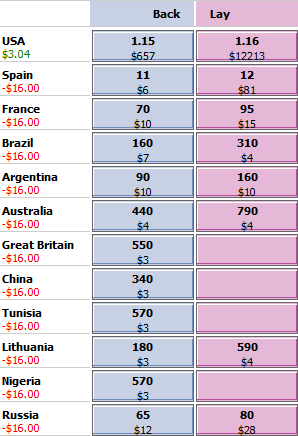
The following are worked examples of the hedging principles above using actual Betfair odds. The market we will use is the ‘Gold Medal Winner’ market for the 2012 men’s Olympic basketball.
At an earlier time a $16.00 wager was made at 1.19 odds on the USA. The lay odds for the USA have since dropped to 1.16. The image to the right shows our position. Because the lay odds are less than our original back odds a hedging opportunity exists.
When such an opportunity arises the first thing we need to do is check the market depth. Note that hedging is easy in this particular market due to the substantial market depth for the USA ($12,213 at lay odds of 1.16).
Given the information above we have:
WB = $16.00 (our initial back wager on the USA)
DB = 1.19 (our initial back odds on the USA)
DL = 1.16 (the current lay odds on the USA)
Note that if we don’t hedge and USA wins we stand to profit:
Profit = WB* (DB – 1)
Profit = $16.00 * (1.19 – 1)
Profit = $3.04 ($2.89 after a 5% commission)
However, if the USA loses we stand to lose $16.00.
We will now compare the outcomes for three hedging strategies:
1. Biased hedge: profit if team USA wins with no loss if team USA loses
2. Biased hedge: profit if team USA loses, with no loss if team USA wins
3. Unbiased hedge: same profit regardless of whether team USA wins or loses
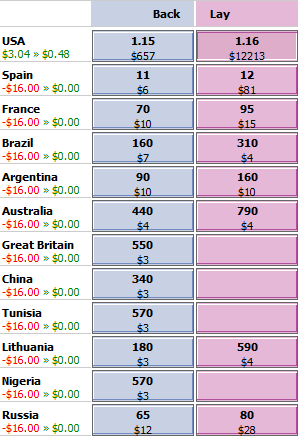
1. Biased hedge: profit if USA wins
Here we seek to avoid a loss if USA doesn’t win. We use equation (3) above:
WL = WB
WL = $16.00
With this strategy our profit if USA wins becomes:
Profit = WB* (DB – 1) – WL* (DL – 1)
Profit = $16.00 * (1.19 – 1) – $16.00 * (1.16 – 1)
Profit = $0.48 ($0.46 after a 5% Betfair commission)
while our profit if USA loses becomes:
Profit = WL – WB
Profit = $16.00 – $16.00
Profit = $0.00
The image to the right illustrates the change in our position. The profit before commission drops from $3.04 to $0.48 if team USA wins, while our profit if the USA loses rises from -$16.00 to $0.00. We now have a chance of making a $0.48 profit with no chance of incurring a loss.
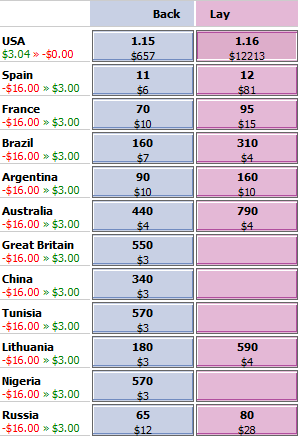
2. Biased hedge: profit if USA loses
Here we seek to avoid a loss if USA does win. We use equation (4) above because our first wager was a back bet.
WL = WB* (DB – 1) / (DL – 1)
WL = $16.00 * (1.19 – 1)/(1.16 – 1)
WL = $19.00
With this strategy our profit if USA wins becomes:
Profit = WB* (DB – 1) – WL* (DL – 1)
Profit = $16.00 * (1.19 – 1) – $19.00 * (1.16 – 1)
Profit = $0.00
while our profit if USA loses becomes:
Profit = WL – WB
Profit = $19.00 – $16.00
Profit = $3.00 ($2.85 after a 5% Betfair commission)
The image to the right illustrates the change in our position. The profit before commission drops from $3.04 to $0.00 if team USA wins, while our profit if the USA loses rises from -$16.00 to $3.00. We now have a chance of making a $3.00 profit with no chance of incurring a loss.
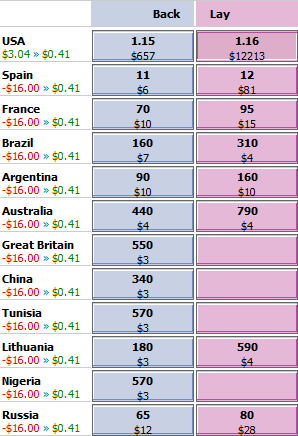
3. Unbiased hedge
Here we seek to achieve the same profit regardless of the event outcome. We use equation (1) above because our first wager was a back bet.
WL = WB* (DB / DL)
WL = $16.00 * (1.19 / 1.16)
WL = $16.41
With this strategy our profit if USA wins becomes:
Profit = WB* (DB – 1) – WL* (DL – 1)
Profit = $16.00 * (1.19 – 1) – $16.41 * (1.16 – 1)
Profit = $0.41 ($0.39 after a 5% Betfair commission)
while our profit if USA loses becomes:
Profit = WL – WB
Profit = $16.41 – $16.00
Profit = $0.41 ($0.39 after a 5% Betfair commission)
The image to the right illustrates the change in our position. The profit before commission drops from $3.04 to $0.41 if team USA wins, while our profit if the USA loses rises from -$16.00 to $0.41. We have a guaranteed profit of $0.41 regardless of the event outcome.
The spectrum of hedging options
The examples above illustrate three hedging strategies: (1) lay $16.00 on team USA, (2) lay $19.00 on team USA and (3) lay $16.41 on team USA. These strategies provide a profit range of $0.00 to $0.48 if team USA wins and $0.00 to $3.00 if team USA loses. In-between these strategies is a spectrum of possibilities. The graph below plots net profit after commission based on the size of the lay bet. A lay bet of $0.00 represents the unhedged position with a possible $2.89 profit after commission if the USA wins and a possible loss of $16.00 if the USA loses.
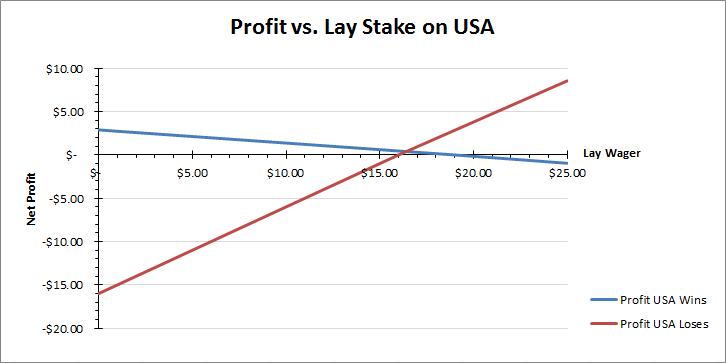
Note that for every lay bet in-between $16.00 and $19.00 a profit is guaranteed regardless of the event outcome. For any lay wager below $16.00 a loss will occur if the USA loses, and for any lay wager above $19.00 a loss will occur if the USA wins. For a lay wager of $16.41 the profit is the same regardless of whether the USA wins or loses. The graph below further highlights region.
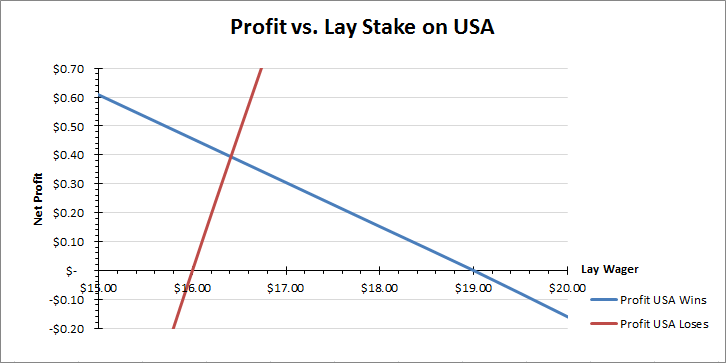
Calculator
Play around with our online hedging calculator to see how the profit opportunities relate to the back and lay odds.
Summary
This section discussed hedge betting using Betfair, with biased and unbiased strategies discussed. Betfair is conducive to hedging due to the user’s ability to back and lay selections. Identifying a hedging opportunity is easy. Hedging is possible whenever the back odds move above the lay odds of a previous wager, or when the lay odds drop below the back odds of a previous wager. A spectrum of strategies can be used, with the discussion here focused on the strategies that are bounded by no profit/loss results if the selection wins or loses.
It is interesting to note the role that odds play on hedging. In the example above a biased hedge towards the USA pays $0.48 if USA wins with no profit or loss if it loses. Due to the short odds on the USA, an unbiased hedge only drops the profit if the USA wins from $0.48 to $0.41, while the profit if the USA loses rises from $0.00 to $0.41.
Below is a summary of the hedging formulas:
Unbiased hedging:
If we had initially made a back wager of amount WB at decimal odds DB and are looking to hedge because the lay odds (DL) are now less than DB, then we calculate the lay wager stake amount WL as:
WL = WB* (DB / DL) (1)
If we had initially made a lay wager of amount WL at decimal odds DL and are looking to hedge because the back odds (DB) are now greater than DL, then we calculate the back wager stake amount WB as:
WB = WL* (DL / DB) (2)
Biased hedging:
The following strategy will provide no profit or loss if the selection doesn’t win:
WL = WB (3)
The following strategy will provide no profit or loss if the selection wins. If we had initially made a back wager of amount WB, then we calculate the lay wager stake amount WL as:
WL = WB* (DB – 1) / (DL – 1) (4)
The following strategy will provide no profit or loss if the selection wins. If we had initially made a lay wager of amount WL, then we calculate the back wager stake amount WB as:
WB = WL* (DL – 1) / (DB – 1) (5)
