Breaking Even on Line Bets – How to Improve Your Chances

While you shouldn’t really isolate week by week performance, it does feel good to end a week with more money in your account than what you started with. It is also good to end in the black if you have placed bets using a substantial portion of your account balance. This article looks at the chances of breaking even for a given number of line bets.

What is a line bet?

 
Line bets are designed to provide equal payouts for each team for a given event. Because one team will have a higher expected chance of winning, line bets are created by adding a predetermined amount to the underdog’s score, or by subtracting that same amount from the favourite’s score. Take, for example, SportsBet odds on Monday’s NBA fixture between the Rockets and the Lakers.

	|	Head to head	|	Line
Houston Rockets	|	8.50	|	1.91 (+12.0)
L A Lakers	|	1.07	|	1.91 (-12.0)

 

The LA Lakers are heavily favoured to win, hence the low 1.07 odds. The line bet provides equal 1.91 odds by giving the Houston Rockets a 12 point head start. At the end of the game, 12 points are added to Houston’s score, and the line bet payouts are determined based on their revised score compared to the LA Laker’s score. Conversely, you can think of it as subtracting 12 from the LA Laker’s score and comparing it to Houston’s original score.

Update: In this case the LA Lakers won the game by 19 points, so the line bet on the Lakers paid out.

How many bets should I make?

 
Line bets are designed to give a 50% chance of winning, but due to bookmaker margins, the offered odds are typically between 1.91 and 1.95. This means you have to win more than 50% of your line bets to achieve a net profit.

I have often setup two line bets, only to realise that I will have to win both of them to earn a profit. By adding a third bet, I will only need to win two out of the three bets to be in the black. So, what number of line bets gives the greatest chance of making a profit?

The table below lists the number and percentage of bets required to earn a net profit from a series of line bets.

Num Bets	|	Req Wins	|	Req %	|	Probability *	|	Prob / Req
1	|	1	|	100%	|	50%	|	50%
2	|	2	|	100%	|	25%	|	25%
3	|	2	|	67%	|	50%	|	75%
4	|	3	|	75%	|	31%	|	42%
5	|	3	|	60%	|	50%	|	83%
6	|	4	|	67%	|	34%	|	52%
7	|	4	|	57%	|	50%	|	88%
8	|	5	|	63%	|	36%	|	58%
9	|	5	|	56%	|	50%	|	90%
10	|	6	|	60%	|	38%	|	63%

 

The first column is the number of line bets made. The second column shows the number of wins required to make an overall profit. The ‘Req %’ column lists the percentage of bets that must win to make a profit. The probability column shows the chance of winning at least that number of bets. The final column shows the ratio of this probability to the percentage of winning bets required. This provides a measure of value, with a higher percentage meaning you have better odds of breaking even.

For example, if you made seven line bets, you would need to win 57% of them. The chance of this occurring (providing the odds on the line bets really are 0.5) is 50%.

There are two trends in the required percentage. First, an odd number of bets requires a lower percentage of correct bets to be profitable than the even bets either side of it. Second, the higher the number of bets (comparing odd numbers to odd numbers, and evens to evens), the lowered the required win ratio.

For the probabilities of making the required number of bets, they are always 50% for an odd number of bets, and less than 50% for even numbers. The higher the even number of bets, the closer to 50% the odds become.

As you can see, it is the most difficult to break even when you make two line bets. If the chance of winning each bet really is 50%, you have a 25% chance of winning both bets, hence you have a 25% chance of securing a profit. This is much worse than the 50% chance if you only made one bet. If you made a third bet you would then only need to win two out of three bets to make a profit. The probability of this happening is 50%, so you have twice as good a chance of making money!

If you’re confused as to why you have a 50% chance of winning at least two out of three bets, consider the possible outcomes:
0 wins
1 win
2 wins
3 wins

There are four possible outcomes, half of which are ‘in the money’. In terms of comparative probabilities:
P(0) = P(3)
P(1) = P(2)

And P(0) + P(1) +P(2) + P(3) = 1

So P(2) + P(3) = P(0) + P(1). Hence you have a 50% chance of winning at least two out of three bets.

Caveats

 
There are two caveats to this theory. First, you shouldn’t isolate performance from week to week. For example, you may decide to make five line bets per week, but over a two week period, this amounts to 10, so you would have had a better chance betting on five in week one and six in week two (providing you were never going to make a line bet again). This theory applies when you only occasionally make line bets. For example if you see two line bets that interest you for a weekend of rugby league, the theory shows you would be better off picking a third line bet to go with them.

Second, this theory assumes you have an equal chance of winning each bet regardless of how many bets you make. In reality, you may have stronger opinions regarding some bets than others. So if you have two bets you feel strongly about, and are looking around for a third line bet to complement them, you may end up picking a bet that has a lower chance of winning than your first two bets.

Notes

 
* The probability of making a profit for a series of line bets is calculated as the odds of making each number of bets over and above what is required. For example, if you have made five line bets, three of those bets must win to make a profit. The probability of achieving this equals the sum of the probabilities of winning 3, 4, and 5 bets. To calculate the probability of winning a particular number of bets, I have used binomial distribution theory. To calculate the binomial coefficient, I have used Pascal’s triangle, although you can use the formula given below. See the links at the bottom of the article for more information.

Binomial probability mass function

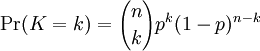
Where n is the number of bets, k is the number of winning bets, and p = 0.5.

Binomial coefficient

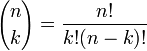
Pascal’s triangle

Sources:
Wikipedia – Binomial distribution
Wikipedia – Pascal’s triangle