Martingale Strategy Applied to Sports Betting

Anyone who has shopped around for casino betting strategies has likely heard of the Martingale betting system. It is a simple strategy where you double your bet size each time you lose, and reset your bet amount to a base level each time you win. The logic behind it is that you have to eventually win sometime, hence you will always return a profit. While this system is mathematically flawed for casino betting, I thought it would be interesting to apply it to sports betting. The fundamental difference between casino betting and sports betting is the real odds of winning aren’t fixed, and there are plenty of sports where long winning streaks are rare.

This article first discusses the Martingale betting strategy as it would apply to a roulette table at a casino. This is followed by Martingale inspired strategies for sport tournaments and other sport scenarios. I have come to the conclusion that if you pick your targets carefully, you can make the system work for you, but the system is by no means risk free, and it requires a substantial amount of funds in your betting account.

What is the Martingale betting strategy?

The martingale strategy can apply to a variety of games such as craps and coin tosses. It is explained below with respect to roulette.

The strategy works by setting a base bet amount, say, $10. You place a bet on red (or black, odds, or evens), which in the American roulette table has a 18/38 chance of winning and a 20/38 chance of losing (47% and 53%, respectively). If you win, you place another $10 bet on the next spin of the wheel. If you lose, you double your bet to $20 for the next spin. If you lose again, you bet $40, then $80, then $160, and so on, until you win. The idea is that streaks of black or green on the roulette table can’t go on forever, so you will have to win sometime, making this a ‘risk free’ way to earn money.

Why the Martingale strategy is flawed (when applied to casinos)

There are two primary flaws with the strategy. The first flaw is that most tables have a betting limit, so if you hit a nasty losing streak you could hit the table limit before you can win back your money. Some casinos, however, do offer no limit tables.

The second, and more fatal flaw, is that if you play the strategy long enough, you have a very good chance of running out of money before winning back your losses. This is because each time you lose on a spin, you increase your bet amount exponentially. The chance of losing six times in a row is (20/38)^6 = 2.1256%, which seems low, but the more spins you play, the odds of this happening increases dramatically.

– In 68 spins there is a 50.3% chance that you will lose 6 times in a row at some point
– In 150 spins there is a 80.6% chance that you will lose 6 times in a row at some point
– In 250 spins there is a 95.3% chance that you will lose 6 times in a row at some point
* Source: Wikipedia

This means you will need $640 left to avoid losing your money after six consecutive losses. Even if you bring $5,000 to the table there is a good chance you will reach six losses in a row on multiple occasions, and each time that happens you could only afford another two losses before running out of money.

You can also mathematically prove the system is flawed. Basically, it only work if the odds of winning are more than 50%, which never occurs in casinos with 1:1 returns. See Wikipedia for a mathematical proof.

Now that the Martingale strategy has been introduced, it will now be discussed with regards to sports betting.

The Martingale strategy applied to sports betting

Three Martingale type strategies will be looked at. The first strategy will be to bet against a player in a tennis tournament. The second strategy will be to bet against a team during the Major League Baseball (MLB) regular season. The third strategy will involve line bets.

Tennis tournament

In a tennis tournament there is typically only a small pool of players who have a reasonable chance of winning. In the current men’s game you would predict the winner of a grand slam to be either Nadal, Federer, Djokovic or Murray.

The Martingale strategy is to pick a player who you are convinced won’t win the tournament. You then consistently bet against this player until he or she is knocked out of the tournament. Each time you lose you will have to bet a larger amount to cover your losses from the previous bets. Because ever larger bets are required as they progress through the tournament, it is critical that you select your player carefully.

Tips for selecting a player

• Pick a player who you wouldn’t expect to get past the first round. You don’t want to still be betting against him or her in the quarter finals unless you have thousands of dollars in your account balance.
• Pick a player who is as far from the highest seeded players as possible. You want someone who will have to play lower seeded players before they reach a top eight opponent. This is critical to avoid a scenario where the odds on them losing is something like 1.08, which can often be the case against a top ranked player. Remember, the lower the odds, the more that must be spent to cover your losses from previous rounds.
• Pick a player that you know and who has a track record of not getting far. Avoid a wild card entry unless you know something about them. This is to avoid a scenario where a young prodigy comes in and reaches a late stage of the tournament.

Let’s say you pick Xavier Malisse to not win a tournament. In his first round he is drawn against James Blake with the following odds. You set your base bet at $10.00.

Malisse — 2.40
Blake — 1.55

Best case scenario

Blake beats Malisse and you win a ($10 x 1.55) – $10 = $5.50 profit. You can then focus on finding new targets.

Good case scenario

Malisse beats Blake and you lose $10.00. The next round’s odds for Malisse’s match against Juan Monaco are as follows.

Malisse — 2.80
Monaco — 1.40

To recoup your $10 in losses you will need to bet at least $10/(1.4 – 1) = $25 on Monaco.

You choose to bet $30 on Monaco and he wins. Your net profit for the tournament is ($30 x 1.40) – $27 – $10 = $5.00.

Bad case scenario

Malisee beats Blake and Monaco to setup an encounter against Juan Martin Del Potro. The odds are as follows:

Malisse — 3.30
Del Potro — 1.30

To recoup your $40 in combined losses you will need to bet at least $40/(1.3 – 1) = $133.33 on Monaco.

You choose to bet $140 on Monaco and he wins. Phew! Your net profit for the tournament is ($140 x 1.30) – $140 – $27 – $10 = $5.00.

Worst case scenario

Malisse wins the tournament! In this case you will have either run out of money sometime before then or you will have managed to lose more on him every round, without ever securing a win. This highlights why it is critical to select your target players carefully.

MLB regular season

In the United States they have sports like the NBA and MLB where the regular seasons seems to go on forever. For this reason it is typically a reasonable assumption that a weak team will lose at least one more game before the season’s end.

In the 2009 MLB season the Washington Nationals currently have a 11 and 28 record (11 wins, 28 losses). Last season they finished the year 59 and 102, which means there are about 122 games left in their 2009 regular season. It is safe to say they will lose at least one game during that time!

The Martingale strategy involves setting a base bet of, say $10.

Washington’s next game is against the Pittsburgh Pirates with the following odds:

Pittsburgh Pirates — 1.98
Washington Nationals — 1.83

If Washington loses you receive $9.80 in profit. You would then bet $10 on their next game. If Washington wins you will have to recoup that loss in their next game against the Baltimore Orioles. If the odds are:

Baltimore Orioles — 1.63
Washington Nationals — 2.20

You would have to bet at least $10/(1.63 – 1) = $16 on Baltimore to recoup your losses.

If you bet $20 on the next game and Baltimore won you would win a $20*1.63 – $20 – $10 = $2.60 profit. If Washington won again you would have to bet more again on the next bet, and so on.

With this strategy you can be reasonably confident that NO team in the MLB will go undefeated through the 100+ games left in the regular season. This means you could choose to target any team. Keep in mind that the lower ranked teams will have lower odds on them to lose, meaning you will have to bet larger amounts to recoup previous losses.

How much money is needed to make this system work?

This all depends on the nature of your targets and your selected sport.

The best way to work this out is to run a scenario analysis. You will need to calculate how long of a losing streak you wish to be capable of handling. You then work out a reasonable base bet amount from there. If you’re like me and only have a access to a few hundred dollars, you will likely start with a $1 or $2 dollar bet. Let’s use the baseball example and say that you are confident Washington will never go on a five game winning streak. With the following odds for them to lose (keeping in mind that the odds will drift higher as their streak develops):
Odds

Game 1 – 1.98 – Washington wins
Game 2 – 1.63 – Washington wins
Game 3 – 1.72 – Washington wins
Game 4 – 2.12 – Washington wins
Game 5 – 1.62 – Washington wins
Game 6 – 2.00

Bets (rounded up)

Game 1: $1.00
Game 2: $1 / (1.63 – 1) = $2.00
Game 3: ($2 + $1) / (1.72 – 1) = $6.00
Game 4: ($6 + $2 + $1) / (2.12 – 1) = $10.00
Game 5: ($10 + $6 + $2 + $1) / (1.62 – 1) = $32.00
Game 6: ($32 + $10 + $6 + $2 + $1) / (2.00 – 1) = $52.00

If Washington lost their sixth game you would secure a profit of ($52 x 2.00) – $52 – $32 – $10 – $6 – $2 – $1 = $21.00.

Your total bet amounts are $103.00, so in this scenario you needed access to more than 100 times your base bet in order to sustain the five game winning streak.

The calculated required amount heavily depends on expected odds. For example, had the odds for game six been 1.20 you would have needed $302.00 in your account. Because the season is so long, you could sit out a game if you don’t like the odds, and wait for better value.

I would recommend following a team closely to establish an expected length of future winning streaks. You could then factor in a safety margin and then calculate your optimal base bet and account balance accordingly.

Martingale strategy applied to line bets

Line bets offer equal payouts to each team, and are designed to have a 50% chance of winning. Because one team will have a higher expected chance of winning, line bets are created by adding a predetermined amount to the underdog’s score, or by subtracting that same amount from the favourite’s score.

For a Martingale strategy applied to line bets, let’s look at it mathematically for one round.

Let q be the probability of losing a line bet. We then define the probability of winning a line bet as (1-q). Let B equal the base level starting bet. Finally, let n equal the number of bets you can afford to lose before running out of money.

The probability of losing all of your bets and running out of money is qⁿ. If you lose all of your bets the amount you would lose is:

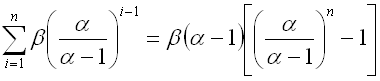
If you do not lose all n bets, you win B (your initial bet amount). The expected profit per round is

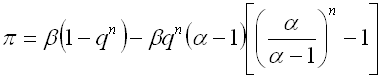
For the profit to be greater than zero, the following must hold:

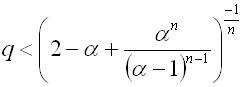
Recall that q is the probability of losing a particular bet, and the probability of winning a bet is 1-q. Below is a table of the required probabilities of winning each bet to provide an expected profit that is greater than zero. Each win probability in the table provides an expected profit of zero for the given n and line bet odds. The results are provided for when the line bet odds are 1.91 and when they are 1.95. These represent two common bookmaker odds on line bets.

n	|	1.91	|	1.95
1	|	0.5000	|	0.5000
5	|	0.5147	|	0.5079
10	|	0.5190	|	0.5103
25	|	0.5218	|	0.5118
50	|	0.5227	|	0.5123
100	|	0.5231	|	0.5126
250	|	0.5234	|	0.5127
500	|	0.5235	|	0.5128

 

The more bets you are able to make, the greater the required probability of winning each bet. Also, the required performance is greater for 1.91 odds than for 1.95 odds. As n approaches infinity, the required win ratio equals the inverse of the odds (i.e. 1/1.95 = 0.5128 and 1/1.91 = 0.5236).

Basically, if you can win line bets more than 53% of the time, you can make this Martingale strategy work for you.

So is the Martingale strategy flawed for sports betting?

If you choose your bets VERY wisely, you can make this system work for you, but it is by no means full proof. You will need to have a substantial amount of funds in your account to make it work, as well as nerves of steel if you make a large run of losses.

Personally, I will give the Martingale strategy a miss.

Sources:
Wikipedia – Martingale betting system