Accounting for the time value of money in betting decisions

Most punters know that in deciding whether to bet, you should first estimate the probability of a particular outcome, and then compare that probability to the inverse of the betting odds. But how many of us factor the time value of money into our betting decisions? I believe this is an important consideration, because any money you lock into a bet can’t be used for other purposes until the event has finished and your winnings are paid out. There is an opportunity cost to this money, the calculation of which is discussed here.

The main result from this article is that the further away the payout for your winning bet, the higher the odds need to be to compensate you for the delay in receiving your funds. Bookmakers typically don’t provide any compensation for this, which means you should bias your betting towards bets with more immediate payouts.

Example without time value of money

Consider a betting decision in the absence of time. Here you compare the inverse of the betting odds to your perceived probability of occurrence. Suppose the odds for the NHL fixture ‘Los Angeles Kings at Vancouver Canucks’ are as follows.
     LA Kings 2.60
     Vancouver Canucks 1.52

The bookmaker’s odds translate to an implied probability of 1/1.52 = 65.8% for Vancouver to win, and 1/2.60 = 38.5% for LA to win. Note that the probability of LA winning equates to a 1 – 38.5% = 61.5% probability of Vancouver winning. At this point, or preferably before you’ve looked at the odds, you determine your expected probability of Vancouver winning, which I will denote P. Your probability can fall within one of three ranges:
     P < 61.5%      61.5% < P < 65.8%
     P > 65.8%

If you believe the probability of Vancouver winning is less than 61.5%, you should bet on Los Angeles. If you personally believe the probability is greater than 65.8%, you should bet on Vancouver. Finally, if you believe the true probability lies between 61.5% and 65.8%, then you should not make a bet on this fixture.

Example with time value of money

In the previous example, the outcome will be determined within a few days of placing a bet, so timing considerations aren’t important. The funds you place on the bet will unavailable for use for only a short period of time. But what if you make a bet on, say, the 2013 Rugby League World Cup? Yes, I know I’ve chosen an extreme example here, but it will illustrate the concept well. Sportsbet’s odds for the three favourites to win the tournament are as follows:
     Australia 1.20
     New Zealand 6.00
     England 8.00

These odd correspond to the implied probabilities below:
     Australia 83.3%
     New Zealand 16.7%
     England 12.5%

You should bet on Australia if your perceived odds of them winning are more than 83.3%, but this ignores the fact that you have made your money unavailable for other uses until after the tournament final in 2013. We clearly need to take this into account before making a betting decision.

How to determine the time value of money

The time value of money equates to the opportunity cost of your betting funds. It is the amount you could earn elsewhere had you not made your bet. This takes into account two things: time and interest rate.

The interest rate is what could get for your money had you chosen not to bet it. I looked at ING Direct this morning, and Australian residents can currently get 4.65% p.a. The time is the date of the expected payout (if your bet wins) minus the date on which you place your bet. Today is the 24th of April, 2010, and let’s assume the 2013 final will take place on November 24th, 2013, so that the payout will be in three years and 7 months time. Mathematically, this is 3 + 7/12 = 3.583 years from now.

We now have the two components with which to calculate the time value of money:
Interest rate = r = 0.0465
Time = t = 3.583

Using the equation 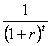we can calculate how much to discount any future payout to arrive at the equivalent value had we won the bet today. Note, to keep things simple I have only compounded the interest once per year. You can learn more about compound interest here.

In our case we get 1/(1.0465)^3.583 = 0.8497 when applying the above formula.

Now that we have determined our discount for the time value of money, we need to multiply the bookmaker odds by this value, and then recompute the implied probabilities:

     Australia 1.20 x 0.8497 = 1.0196
     New Zealand 6.00 x 0.8497 = 5.0982
     England 8.00 x 0.8497 = 6.7976

The new implied probabilities are:

     Australia 98.1%
     New Zealand 19.6%
     England 14.7%

This means that instead of betting on Australia if you believe the odds are over 83.3%, you should only consider betting if your perceived odds are over 98.1%. These required probabilities are drastically higher because if you put your money into a savings account you could get the equivalent of 1.0465^3.583 = 1.1769 odds without taking any risks! Note that 1/0.8497 = 1.1719.

General formula

Below is a general formula for comparing adjusted betting odds to your perceived probability of occurrence. Note that I have used the property (1/x)/(1/y) = y/x. Play around with the formulas to verify the result for yourself.

P_X = your perceived probability of outcome X occurring.
B_X = the bookmaker odds for outcome X
B_X^C = bookmaker odds for outcome X to not occur (where available)
L denotes “low”
H denotes “high”
NB denotes “no bet”

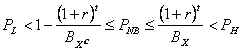
When you can bet either for or against outcome X, like in a hockey game, your decision is based on the comparisons below:

If P_X < P_L then you should bet AGAINST outcome X
If P_X > P_H then you should bet on outcome X
If P_X = P_NB where P_L < P_NB < P_H then you should not bet on the event

When you can’t easily bet against outcome X, like for the Rugby League World Cup winner, your decision is based on the equation below:

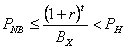
If P_X > P_H then you should bet on outcome X
If P_X = P_NB where P_NB < P_H then you should not bet on the event.

Closing remarks

While the Rugby League example I have used is extreme, I honestly believe that you should take into account the time value of money when making bets that are to take place more than three months away. For three months your time is 3/12 = 0.25, so you should multiply the available odds by 1/1.0465^0.25 = 0.9887 before comparing them to your perceived probability of occurrence. Looking again at our LA Kings vs Vancouver Canucks example, if the fixture was to take place three months from now, the range for which you would not bet would expand from 61.5% < P < 65.8% to 61.1% < P < 66.5%. Note that the range of perceived probabilities for which you would not bet always expands when you factor in the time value of money. At this stage I must point out some caveats: First, the above analysis assumes that you are 100% confident that your estimated probability is correct. In reality, there is uncertainty in your probability estimate. For example, you may guess that probability of an outcome is 60%, but believe that the true probability could lie anywhere between 50% and 70%. It turns out that the decision of whether to bet is independent of your confidence in the probability estimate. The decision of how much to bet will take into account this uncertainty. I will discuss the issue of how much to bet, which directly relates to your confidence in the estimated probability, on a later date. Second, most sports punters are pure gamblers. Few consider withdrawing money from a sports betting account and putting into a bank account. This makes the use of a savings account interest rate as an opportunity cost irrelevant. I suppose I'm reaching out to a more rational sports betting audience here. Most likely, any decision not to bet simply frees up money to bet elsewhere. In this case your opportunity cost is actually a comparison between two possible bets. If you are constrained for funds, you could bet on event E₁ that takes place t₁ days time, or you could bet on event E₂ that takes place in t₂ days time. You would need to discount one using the expected payoff from the other to determine whether to bet on it. Another option is to look at your historical betting performance, and determine an expected return on your betting account each year. If it is 20%, then a bet on an event that pays out one year from now should have the odds discounted by 1/1.2 first. Of course, the downfall of this method is that many punters have negative earnings history, which would lead to erroneous results.

The analysis here is intended to provide food for thought. The main concept is that the further away the payout for your winning bet, the higher the odds need to be to compensate you for the delay in receiving your funds. Bookmakers typically don’t provide any compensation for this, which means you should bias your betting towards bets with more immediate payouts. This result draws from the fact that the P_NB region expands as t increases, making you less inclined to make a wager on later fixtures.