Kelly Criterion – Part 1 – Introduction

In an earlier post I showed how to determine whether to place a bet on a particular sporting outcome. While the post discussed whether to bet, it didn’t determine how much to bet.

This post will serve as the first of a series to discuss the Kelly criterion. They Kelly criterion is a formula used to determine how much of your money to place on a particular gamble. The formula was derived by J.L. Kelly, Jr in 1956. The formula has a number of applications, one of which is sports betting.

This post provides an introduction to the Kelly criterion. At this stage, my intention for the rest of this series is as follows:
– Part 2 will provide a simple derivation of the formula
– Part 3 will discuss some extensions to the model

The formula

The formula calculates the fraction, f, of your account balance that you should place on a bet, given the available odds and your perceived probability of winning. The formula depends on how you express the betting odds, so I have provided two versions below. Version A uses the decimal odds system that is popular in Australia. Decimal odds of 2.50 mean that if you win, a $10 bet would result in a $25 payout and a $15 profit. Version B uses the “b to 1” odds system, where odds of “3 to 1” mean that if you win, a $10 bet would result in a payout of $40 and a profit of $30.

Version:		A		B
Formula: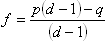
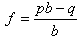Variables:		f = fraction of your bankroll to bet d = decimal betting odds p = probability of bet winning q = 1 – p = probability of bet losing		f = fraction of your bankroll to bet b = “b to 1” betting odds p = probability of bet winning q = 1 – p = probability of bet losing

 

The betting odds are observable and easy to obtain. The key variable in this formula is the probability, p, of the bet winning. Observe that q is simply 1 – p. So if the probability of winning is 60%, then the probability of losing must be 40%. Note that this ignores the chance of a refunded bet. If you play around with the formula you will find that the greater your perceived odds of winning, relative to those implied by the bookmaker, the larger the percentage of your account you should bet. The probability implied by the bookmaker for a particular outcome is the inverse of the decimal odds. For example, 2.50 odds imply a 1/2.5 = 40% chance of winning.

A worked example

The example below uses the decimal odds system. To obtain b, if that’s what your most comfortable using, simply subtract 1 from d.

Suppose you observe the following odds for the football game between Arsenal and Chelsea.

Full-time result:
Arsenal: 2.60
Chelsea: 2.65
Draw: 3.25

You take a look at the current form of the two sides, and believe the probabilities of the respective outcomes are as follows:

		p		q
Arsenal		20%		80%
Chelsea		50%		50%
Draw		30%		70%
		——-
Total		100%

 

Hence, in your opinion, there is a 20% chance of Arsenal winning, a 50% chance of Chelsea winning, and a 30% chance of a draw.

Note that the sum of p an q for each outcome is 100%. Also note that the sum of the values for the p’s also equals 100%. Using the Kelly criterion, you calculate the optimal fraction of your wealth to bet on each outcome as follows:

Arsenal: f_A = [0.2(2.6 – 1) – 0.80]/(2.6 – 1) = -0.300
Chelsea: f_C = [0.5(2.65 – 1) – 0.50]/(2.65 – 1) = 0.197
Draw: f_D = [0.3(3.25 – 1) – 0.70]/(3.25 – 1) = -0.011

Because the fractions f_A for Arsenal and f_D for the Draw are below zero, you would not bet on these outcomes. The fraction, f_C, for Chelsea is a positive value of 0.197. This means you should bet 19.7% of your betting account balance on Chelsea to win. If your account balance is currently $200, then you should place a $39.40 bet on Chelsea.

Note that if your probabilities for Arsenal, Chelsea and a draw were 35%, 35% and 30%, respectively. Then you would not make any bet on this event. Plug the corresponding probabilities into the formula to verify this result for yourself.

Coming up in Part 2

This post simply provides the formula and illustrates how to use it. The derivation of the formula will be discussed in Part 2. To give you some idea of the methodology, the Kelly criterion aims to maximise the log of the expected growth rate of your account balance.

Sources:

• Wikipedia – Kelly Criterion
• Original paper by Kelly: A New Interpretation of Information Rate