This post is Part 2 of a series on the Kelly criterion and its application to sports betting. Part 1 of this series provides an introduction to the Kelly criterion along with a worked example. This post provides a simple derivation of the Kelly criterion, which will hopefully provide additional insight into the model. Please read Part 1 before proceeding, if you have not done so already.
The proof below uses the decimal betting odds system. To use the “b to 1” odds system, simply replace d with b + 1 in the workings below. Please note that this is not a rigorous proof. Readers should consult Kelly’s original paper for a formal derivation of the Kelly criterion.
Notation
We will continue with the notation used in Part 1. Let:
f = the fraction of your bankroll (account balance) to bet on a particular outcome of a sporting event (where 0 < f < 1) d = decimal betting odds for that outcome (2.50 means a winning $10 bet would have a payoff of $25 and a profit of $15) p = your perceived probability of the bet winning (where 0 < p < 1)
q = 1 – p = probability of the bet losing
Furthermore, let W0 denote your account balance today, and let Wn denote your account balance after the settlement of n bets. Both W0 and Wn are in monetary units.
Derivation
Suppose you have an account balance, W0 and have the option of betting a on a sporting outcome that pays odds of d. You believe that the probability of this outcome occurring is p. What fraction, f, of your account balance should you place on this bet?
If you win, your bet will result in a payout of f*W0*d. This corresponds of a profit of f*W0*(d-1). If you lose, then your bet results in a payout and profit of –f*W0, which is a loss.
At the end of your bet, your new bankroll will be:
W1 = W0 + f*W0*(d-1) = W0(1 + f*(d-1)) if you win, and:
W1 = W0 – f*W0 = W0(1 – f) if you lose
Now suppose you make the same bet two times. If you win both bets, you end up with:
W2 = W0(1 + f*(d-1))(1 + f*(d-1)) = W0(1 + f*(d-1))2
This is because your initial bankroll after the first bet is W1(1 + f*(d-1)) instead of W0.
If you lose both bets, you end up with:
W2 = W0(1 – f)(1 – f) = W0(1 – f)2
This is because your initial bankroll after the first best is W1(1 – f) instead of W0.
If you win the first bet and lose the second, you end up with:
W2 = W0(1 + f*(d-1))(1-f)
Note that this is the same value as if you had lost the first bet and won the second. This result holds true for any series of bets in this setup. If you win x times and lose y times, the order of the wins and losses is irrelevant to the final outcome.
Observe that (1 + f*(d-1)) is the multiplier whenever a win occurs, and (1-f) is the multiplier whenever a loss occurs. So, after 8 games, if you won 5 times and lost three times you would end up with:
W8 = W0(1 + f*(d-1))5(1 – f)3
If we generalise this to playing the game n times and winning k times, we have:
Wn = W0(1 + f*(d-1))k(1 – f)(n-k)
When we divide both sides of the equation by W0, we have an expression for the growth of our initial bankroll.
Wn/W0 =(1 + f*(d-1))k(1 – f)(n-k)
This equation gives us the growth or our bankroll after n games. To calculate the growth in the bankroll per game, we need to raise both sides of the equation by a power of 1/n. To illustrate why we do this, suppose you invested $100 that returned $144 after two periods. If you wanted to know the growth rate per period, you would calculate it as follows:
144 = 100*(1+growth)2
144/100= (1+growth)2
1.44 = (1 + growth)2
We now raise both sides of the equation by 1/n, which is 1/2 in this case. This enables us to solve for the growth rate.
1.441/2 = (1 + growth)2*1/2
1.2 = (1 + growth)
0.2 = growth
growth = 20%
Hence a growth rate of 20% results in a balance of $144 after two periods.
Returning to our example:
Wn/W0 =(1 + f*(d-1))k(1 – f)(n-k)
(Wn/W0)1/n = [(1 + f*(d-1))k(1 – f)(n-k)]1/n
The Kelly criterion seeks to maximise the exponential rate of growth per game, hence we seek to maximise the log of (Wn/W0)1/n. We achieve this by choosing the optimal fraction of our wealth to bet: f.
In Kelly’s original paper he expressed “the exponential rate of growth of the gambler’s capital” as (pg. 919):
Note that this is consistent with our workings because a known property of logs is log(Wn/W0)1/n = (1/n)*log(Wn/W0).
(1/n)*log(Wn/W0) = log[(1 + f*(d-1))k(1 – f)(n-k)]1/n
Let G = (1/n)*log(Wn/W0). Using known properties of logs we get:
G = (1/n)log[(1 + f*(d-1))k(1 – f)(n-k)]
G = (1/n)[k*log(1 + f*(d-1)) + (n-k)*log(1 – f)]
Anyone who remembers their calculus will recall that if we seek to maximise a function by choosing the optimal value for f, then we need to take the first derivative of the function with respect to f, and set it equal to zero.
Note that if our perceived probability p of success is true, then in the limit as n approaches infinity, we have p = k/n and q =(n-k)/n. Recall that k is the number of successes out of n games, and (n-k) is the number of failures out of n games.
Noting that p + q = 1 and solving for f gives:
Recall that this solution is for the decimal odds system that is popular in Australia. If you use the "b to 1" odds system then the corresponding formula is.
You can take my word for it that this value for f corresponds to a unique maximum for G(f) on [0,1). A formal proof of this can be found here.
Note that if f < 0, then you would anticipate a loss by placing a bet at the available odds. Hence in this circumstance you would bet nothing, and the optimal fraction, f, equals 0. However if you had a Betfair account you may choose to lay a bet against the outcome, although you would have to recalculate f using a model that pays odds of 2.00 if the outcome does not occur, and costs you the lay odds if the outcome does occur. This extension of the Kelly criterion will be discussed in Part 3 of this series.
Coming up in Part 3
Part 3 will provide some extensions to the Kelly criterion. At this stage I may actually break it down into a number of posts. The extensions will be:
– 3a – the Kelly criterion for lay bets in Betfair
– 3b – the Kelly criterion that accounts for the time value of money
– 3c – the Kelly criterion when refunds are a distinct possibility
– 3d – fractional Kelly betting

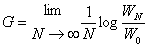
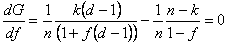
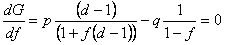
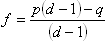
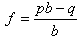
Pingback: Australia Sports Betting » Blog Archive » Kelly Criterion – Part 1 – Introduction
Pingback: Australia Sports Betting » Blog Archive » Kelly Criterion – Part 3a – Backing and Laying Bets with Betfair
Pingback: Australia Sports Betting » Blog Archive » Kelly Criterion – Part 3b – Accounting for the Time Value of Money
Pingback: Australia Sports Betting » Blog Archive » Kelly Criterion – Part 3c – Incorporating the Possibility of a Refund
Pingback: Australia Sports Betting » Blog Archive » Kelly Criterion – Part 3d – Fractional Kelly Betting
Thank you so much, this was truly helpful.
I have a question, when we arrive to Wn/W0 =((1 + f*(d-1))^k)((1 – f)^(n-k)) why don’t we differentiate directly, to get the maximun Wn/W0? Why would you want to find the maximun exponential growth?
That’s a good question. My guess is Kelly did this to remove the variable n (the number of bets/trials) from the final solution for f. As n approaches infinity, we have p = k/n and q =(n-k)/n. The approach enabled Kelly to substitute out n from the equations and create a formula for f that contains p, q and d only.