This post continues Part 3 of a series on the Kelly criterion and its application to sports betting. Part 1 provides an introduction to the Kelly criterion along with a worked example. Part 2 provides a simple derivation of the Kelly criterion. Part 3a extends the Kelly criterion to incorporate backing and laying bets using an exchange such as Betfair. This post extends the Kelly criterion to account for the time value of money. It is recommended that you read Part 1 and Part 2 before proceeding, if you have not done so already.
What is the time value of money?
The time value of money is the concept that a dollar today is worth more than a dollar in the future. If someone offered you a choice between receiving $1,000 now and receiving $1,000 in a year’s time, you would prefer to receive the money today. This is because even if you don’t need the money now, you can earn interest on the $1,000 between now and next year.
The time value of money depends on two variables: time and interest rate. The greater the time until you receive a payment, the less that payment is worth. This is because you have to forgo additional time that the money could be sitting in an interest bearing account. Also, the greater the interest rate, the less the payment in the future is worth. This is because money in a high interest account would have grown by a larger amount in the meantime had you received it now.
In essence, the time value of money relates to the opportunity cost of the funds. By receiving $1,000 in a year’s time instead of today, you have lost the opportunity to earn interest on that money in the meantime.
Visit Wikipedia to learn more about the time value of money.
The implication of time in sports betting
With sports betting, punters have access to a wide range of betting options for events around the globe. These bets can vary drastically in terms of the time it takes for settlement to occur. Settlement is the process of determining whether your bet has won or lost. Obviously, settlement can only occur after the conclusion of the sporting fixture. Typically, most bookmakers settle your bets within minutes of the end of the sporting event. For some events, settlement occurs within a few seconds of the conclusion of the fixture.
Below is a selected list of betting options and their associated settlement dates. Note that this post was written at 2pm on July 21, 2010.
| Event | Settlement date | Approximate time (years) |
| Forex Market Movement | 5 minutes or less | 9.51E-06 |
| ATP Atlanta Tennis Fixture | 6:00 AM July 22nd 2010 | 0.0018 |
| Tour de France winner | July 25th 2010 | 0.011 |
| Tri Nations Winner | September 11th 2010 | 0.14 |
| Rugby World Cup 2011 Winner | Octboer 23rd 2011 | 1.26 |
| FIFA World Cup 2014 Winner | July 13th 2014 | 3.98 |
For fixtures that settle within the next week or so, the time value of money can be safely ignored. However for tournaments that are held in upcoming years, the time value of money is an important consideration.
This post will illustrate that for fixtures that settle in the distant future, the optimal bet amount drops. The conclusion is that you should bias your betting towards fixtures that conclude sooner rather than later.
Notation
This post continues with the notation used in Part 1 and Part 2. Let:
- W0 = your account balance before you make a bet
- Wn = your account balance after making n bets
- f = the fraction of your bankroll (account balance) to bet on a particular outcome of a sporting event
- d = decimal betting odds for that outcome (2.50 means a winning $10 back bet would have a payoff of $25 and a profit of $15)
- p = your perceived probability of an outcome occurring (where 0 < p < 1)
- q = 1 – p = probability of that outcome not occurring
We will introduce some new notation for this post. Let:
- r = the annual interest rate that you could get if you invest your funds elsewhere
- t = the time, measured in years, between now and the settlement of the bet
Calculating the time value of money
If you were given the choice of receiving $1,000 today or $x,xxx in three year’s time, what future figure would make you indifferent between your two options? Most people would turn down $1,001, and most would accept $3,000. If you could invest $1,000 at an interest rate of 5%, then you would have $1,000(1.05) = $1,050 in a year’s time. If you reinvested that figure for the second year you would have $1,050(1.05) = $1,102.50 in two years time. If you reinvested that figure for the third year you would have $1,102.50(1.05) = $1,157.63 in three years time. This means you would have to be offered at least $1,157.63 to consider taking the future amount rather than the $1,000 today.
We can recalculate this figure as $1,000(1.05)3 = $1,157.63. More generally, let PV (present value) denote a payment today, and let FV (future value) denote the future payment that is of equivalent value to the PV. We can calculate the FV as FV = PV(1+r)t. If we knew the FV and wanted to know the PV, we could calculate PV = FV/(1+r)t. Note that this is identical to the mathematical statement PV = FV(1+r)-t.
For those who have a stronger mathematics background, you may prefer to use an exponential interest rate to be consistent with the Kelly criterion’s objective of maximizing the exponential growth rate of your sporting account balance. In this case FV = PV*ert and PV = FV*e-rt. Note that the value for r in this formula will be slightly lower than that used in the previous paragraph, because it is the continuously compounded rate.
To make the workings understandable for a greater audience, PV = FV/(1+r) will be used henceforth. Simply substitute this expression with PV = FV*e-rt if you wish instead to use a continuously compounded rate.
The Kelly criterion revisited
Recall that in Part 2 the exponential rate of growth of the gambler’s capital is expressed as:
(1/n)*log(Wn/W0) = log[(1 + f*(d-1))k(1 – f)(n-k)]1/n
The blue text represents the gross return for a win and the red text represents the gross return for a loss. Let $x denote the dollar value of a bet that you make. In terms of cash flow timings, a losing bet can be treated as occuring immediately. You make your bet of $x, which is taken from your account balance today and never returned. If you make a winning bet, you have $x taken from your account balance today and $x(d-1) returned to your account balance at some point in the future, where d are the decimal odds of your bet. You can think of this as an investment. You deposit $x now and receive $x(d-1) in the future. This payment in the future (FV) must be discounted to get our PV using the formula PV = FV/(1+r).
When we take into account the time value of money, the gross return for winning becomes (1 + f*(d-1)/(1+r)t)k, while the gross return when your bet loses remains unchanged. If you plug this expression into the workings in Part 2 and solve for f, you get:
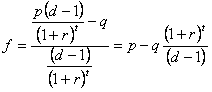
The formula above is for the decimal odds system that is popular in Australia. For those who are more familiar with the “b to 1″ betting odds used in other literature, the corresponding formula is:
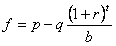
Observe that as r and t increase, the value of f decreases.
The Arsenal vs Chelsea fixture revisited
Recall the hypothetical Arsenal vs Chelsea fixture that was used in Part 1. To recap, the odds are as follows, with your perceived probabilities of occurrence shown in brackets:
Full-time result:
Arsenal: 2.60 (pA = 20% chance of occurring)
Chelsea: 2.65 (pC = 50% chance of occurring)
Draw: 3.25 (pD = 30% chance of occurring)
Based on the Kelly criterion, you should bet
f = [0.5(2.65 – 1) – 0.50]/(2.65 – 1) = 0.197 = 19.7% of your account balance on Chelsea.
We will now recalculate the optimal bet amount assuming that the fixture will take place: in (A): 3 day’s time, (B): 30 day’s time, (C): 1 year’s time, and (D): 3 year’s time. Assume you can get 5% per annum in an interest bearing account. Using the formula above we get:
(A): t = 3/365 = 0.008219
(B): t = 30/365 = 0.08219
(C): t = 1
(D): t = 3
f(A) = 0.5 – 0.5(1.050.008219)/1.65 = 0.197
f(B) = 0.5 – 0.5(1.050.08219)/1.65 = 0.196
f(C) = 0.5 – 0.5(1.051)/1.65 = 0.182
f(D) = 0.5 – 0.5(1.050.008219)/1.65 = 0.149
Hence, for fixtures within the next month or so, you can pretty much ignore the time impact of money unless you are making substantially large bets. However, for events that conclude more than a year from now, the time value of money becomes an important consideration.
You may find that your optimal bet size drops below zero, meaning you shouldn’t make a bet at all. Consider the 2014 FIFA World Cup. You can get odds of 4.50 with bet365 for Brazil to win the tournament. Suppose you believe that Brazil has a 1 in 4 chance of winning. Ignoring the time value of money, you would calculate your optimal bet as:
f = [(0.25)(4.50 – 1) – 0.75]/(4.50 – 1) = 0.036
This means you would bet 3.6% of your account balance on Brazil to win the tournament.
However, if you consider the time value of money, where t = 3.98 and r = 5%, your optimal bet size becomes:
f = 0.25 – 0.75*1.053.98/3.5 = -0.01
Hence, if the time value of money is taken into account, you would chose not to place a bet on Brazil.
Coming up in Part 3c
The next post will provide an extension to the Kelly criterion when refunds are a distinct possibility. For example, bet365 refunds losing football (soccer) bets in the event of a 0-0 draw.