This post continues Part 3 of a series on the Kelly criterion and its application to sports betting. Part 1 provides an introduction to the Kelly criterion and a worked example. Part 2 provides a simple derivation. This post extends the Kelly criterion to incorporate the possibility of a refund. It is recommended that you read Part 1 and Part 2 before proceeding.
Introduction
In the Kelly betting framework, recall from Part 2 the variable p (the probability that an outcome will occur) and the variable q = 1 – p (the probability that the outcome will not occur). If you are betting on this outcome, you believe you will win with probability p, and lose with probability q.
Note that q is defined as 1 – p to ensure that p + q = 1. This implies that no other outcome is possible: you either win or lose. There are, however, bets where refunds are a distinct possibility. In this case there are three possible outcomes and p + q < 1. This post will show that only a slight tweak to the Kelly criterion is required to incorporate the possibility of a refund.
When are refunds a possibility?
Refunds are a distinct possibility for sports such as:
- Football (soccer)
bet365 refunds all losing pre-match Correct Score, Half-Time/Full-Time and Scorecast bets in the event of a 0-0 draw. - Tennis
Each bookmaker has it’s own policy, but Sportsbet, among others, refunds all bets if a player retires injured. Note that Betfair does not do this, which is something to keep in mind when comparing odds. - Boxing
For example, Sportsbet refunded losing bets on the Green v Briggs bout. - Promotions
For popular events bookmakers often run promotions where they refund certain losing bets in the event of a particular outcome. Some of these refunds are announced without warning. For the 2010 FIFA World Cup winner, Sportsbet refunded all losing bets on Australia because they felt the red cards Australia received were harsh.
Notation
This post continues with the notation used in Part 1 and Part 2. Let:
- W0 = your account balance before you make a bet
- Wn = your account balance after making n bets
- f = the fraction of your bankroll (account balance) to bet on a particular outcome
- d = the decimal betting odds for that outcome (2.50 means a winning $10 back bet would have a payoff of $25 and a profit of $15)
- p = your perceived probability of that outcome occurring (where 0 < p < 1)
- q = your perceived probability of that outcome not occurring (where 0 < q < 1 and p + q < 1)
A new variable is introduced in this post. Let:
- j = your perceived probability of receiving a refund (where 0 < j < 1 and p + q + j = 1)
Incorporating the possibility of a refund
In the Kelly betting framework we now have three possible outcomes:
– win (d-1)f with probability p
– lose f with probability q
– have the bet refunded with probability j
The account balance after making one bet can be one of three possible values:
– W1 = W0(1 + f*(d-1)) with probability p
– W1 = W0(1 – f) with probability q
– W1 = W0 with probability j
Recall that in Part 2 the exponential rate of growth of the gambler’s capital was expressed as:
(1/n)*log(Wn/W0) = log[(1 + f*(d-1))k(1 – f)(n-k)]1/n
The blue text represents the gross return for a win and the red text represents the gross return for a loss. Note that in the event of a refund, the account balance is unchanged, so W1 = W0 and W1/W0 = 1. If, after n bets, you had k wins, m refunds, and n-k-m losses, then this expression can be modified to be:
(1/n)*log(Wn/W0) = log[(1 + f*(d-1))k(1 – f)(n-k-m)(1)m]1/n
The number 1, raised to any power, is simply 1 so this expression simplifies to:
(1/n)*log(Wn/W0) = log[(1 + f*(d-1))k(1 – f)(n-k-m)]1/n
Note that for a sufficiently large n, (n-k-m)/n = q. If you plug the expression above into the workings in Part 2 and solve for f, you get:
Note that when q + p = 1 this expression simplifies to the standard Kelly criterion discussed in Part 1 and Part 2. Also note that the denominator term (p + q) could be rewritten (1 – j), where j is the probability of a refund.
The formula above uses the decimal odds system that is popular in Australia. For those who are more familiar with the “b to 1″ betting odds used in other literature, the corresponding formula is:
Interpretation
The impact of a potential refund depends on whether it reduces the possibility of winning, reduces the possibility of losing, or both. With football betting on bet365, the 0-0 draw refund has no impact on the possibility of winning, but it does reduce the possibility of losing, because the refund only applies to losing bets.
In tennis betting, if the bookmaker voids and refunds all bets in the event of injury, this reduces the probabilities of winning and losing because both players have the potential to retire injured. Having said that, it’s not uncommon for players to pick up a an injury during a tournament, but continue playing. You may feel that the injured player is more likely to withdraw hurt than their opponent. This would have an asymmetric impact on your perceived probabilities of winning and losing. Another point to consider is, for someone playing with an injury, there may be a higher chance they will retire hurt if they are losing the match, than if they are winning.
The Arsenal vs Chelsea fixture revisited
Recall the hypothetical Arsenal vs Chelsea fixture used in Part 1. To recap, the odds are as follows, with your perceived probabilities of occurrence shown in brackets:
Full-time result:
Arsenal: 2.60 (p = 20% chance of occurring)
Chelsea: 2.65 (p = 50% chance of occurring)
Draw: 3.25 (p = 30% chance of occurring)
Based on the standard Kelly criterion, you should bet
f = [0.5(2.65 – 1) – 0.50]/(2.65 – 1) = 0.197 = 19.7% of your account balance on Chelsea.
Now pretend the bookmaker refunds all losing full-time bets in the event of a 0-0 draw. Suppose you believe there is a 5% chance of a 0-0 draw, and you believe the outcome probabilities are now:
- Arsenal: 2.60
p = 20% chance of winning, q = 75% chance of losing, j = 5% chance of a refund - Chelsea: 2.65
p = 50% chance of winning, q = 45% chance of losing, j = 5% chance of a refund - Draw: 3.25
p = 30% chance of winning, q = 70% chance of losing, j = 0% chance of a refund
Based on the Kelly criterion, after adjusting for the possibility of a refund, you should bet
f = [0.5(2.65 – 1) – 0.45]/[(2.65 – 1)(0.5 + 0.45)] = 0.239 = 23.9% of your account balance on Chelsea.
The optimal bet size has increased in this example because the perceived probability of losing has dropped.
Coming up in Part 3d
Part 3d will discuss fractional Kelly betting.

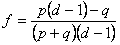
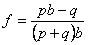
Pingback: Australia Sports Betting » Blog Archive » Kelly Criterion – Part 3b – Accounting for the Time Value of Money