You are here: Home >> Beginner’s Guide >> The Basics >> Implied Probability and Expected Return
When viewing bookmaker odds, it is important to have a means of determining which betting options are good value and which are not. Your methodology will need to compare the bookmaker odds to your perceived probability of each outcome.
Probability is a measure of how likely an event will happen, and can take a value between 0 (0%) and 1 (100%). A value of 0 means the outcome is impossible, and a value of 1 means the outcome is certain. A fair coin toss has a 50% probability of returning heads, while a fair die has a 1/6 = 16.67% chance of returning a 3. It will take some time to get into the habit of assigning probabilities to outcomes, such as a draw in a football game, but it’s important that you do so to assess the value of bookmaker odds.
This section outlines two means by which you can evaluate bookmaker odds. The two methods are actually doing the same thing, but from different approaches.
Note that if there are more than two possible outcomes for an event, your best strategy may be to back more than one outcome. It should also be pointed out that this section enables you to determine whether you should place a bet. It does not address how much of your account balance to wager. More formal betting strategies and the Kelly Criterion will be discussed in Sections 10 and 11 of this guide.
Implied probability
Implied probability is the probability of an outcome occurring as implied by the bookmaker odds. If you believe the chance of a bet winning is higher than its implied probability then you believe the bet is good value. Conversely, if you think the chance of winning is less than the implied probability then you should not make a wager. What you are essentially doing is comparing your opinions to that of the bookmaker. If you believe Team A is more likely to win than the bookmaker does then you will back Team A.
The decimal odds system makes calculation very easy. Simply take the reciprocal of the odds to calculate the implied probability for a particular outcome. Below are some examples:
| Decimal Odds | Calculation | Implied Probability |
|---|---|---|
| 1.50 | 1/1.50 | 66.67% |
| 2.00 | 1/2.00 | 50% |
| 3.00 | 1/3.00 | 33.33% |
Suppose the odds to win a coin toss in a cricket test match are 1.95 for Australia and 1.95 for England. The implied probability for both outcomes (because they have the same odds) is 1/1.95 = 51.3%. Hence you should only place a bet if you believe a team has more than a 51.3% chance of winning the toss. In reality, you know that each team only has a 50% chance of winning, hence you should not place a bet.
In any given example, just because you should not be on outcome A, this does not necessarily imply you should bet on outcome B. Suppose the odds for a basketball game are as follows, with the implied probability of each outcome in brackets:
Miami Heat: 2.10 (1/2.10 = 47.6%)
Chicago Bulls: 1.76 (1/1.76 = 56.8%)
Note that based on the Miami odds, the implied probability for Chicago to win is 1 – 47.6% = 52.4%, and not 56.8% as given by the Chicago odds. Your betting decision is based on how your perceived probability of Chicago winning compares to the implied probabilities given by both the Miami and Chicago odds:
[back Miami range] < 52.4% < [do not bet range] < 56.8% < [back Chicago range]
The preceding example is an event with two possible outcomes. Now consider a three-outcome, head to head, football market on Manchester City vs. Stoke City. Your perceived probability for each outcome is provided in the right column.
| Outcome | Bookmaker Odds | Implied Probability | Comparison | Your Perceived Probability |
|---|---|---|---|---|
| Manchester City Win | 1.36 | 73.5% | > | 60% |
| Draw | 4.75 | 21.1% | < | 25% |
| Stoke City Win | 9.00 | 11.1% | < | 15% |
| Totals: |
105.7%
|
100%
|
||
In this example you would choose to bet on both a draw and a Stoke City win.
Note that your perceived probabilities should always sum to 100%, while the implied probabilities always add to more than 100%. This discrepancy is due to the bookmaker margin, which will be discussed in Section 4 of this guide. The bookmaker margin is a measure of the bookmaker’s profit margin for an event, and is the reason why a scenario exists where you would choose to not place a bet.
There are cases where you would choose to back every possible outcome. This could be when two or more bookmakers offer conflicting odds. In this scenario the sum of the implied probabilities would equal less than 100%. This creates an arbitrage opportunity, which will be discussed in Section 8.
Expected return
Another means of assessing the value of bookmaker odds is to calculate the expected return for each possible outcome. This approach yields the same results as implied probabilities, because it makes the same comparisons, but from a different angle.
Expected return is the expected net profit on your wager. The net profit is your bet winnings after you subtract your initial wager from the total payout. For example, with a winning $10 bet at 2.40 odds, your total payout is $24 for a net profit of $14. This equates to a $14/$10 = 140% return.
Expected return is distinct from potential return, which is the profit received should you actually win. Expected return instead multiplies each potential outcome by its probability of occurrence. For example, suppose you believe a bet at 2.40 odds has a 50% chance of winning. The potential return is 140%, while the expected return is (140% * 50%) = 70%.
In general terms, the expected return is a weighted average of all possible returns, where each weighting equals the probability of its associated return. It is calculated using the following formula, where Ri is the net return for outcome i, and Pi is the probability that outcome i will occur. 1
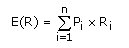
Let’s apply this formula to a finance example. Suppose you believe a given investment has a 50% chance of earning a 10% return, a 25% chance of earning 20% and a 25% chance of incurring a 10% loss, the expected return is calculated as:
(0.50)*(0.10) + (0.25)*(0.20) + (0.25)*(-0.10) = 0.075 = 7.5%
It should be emphasised that these probabilities are not actually known, they are only estimated. This is why we use the expression expected return. The probabilities, and hence the expected return, are based on your expectations.
In a sports betting context, to calculate the expected return from a bet, simply multiply the odds by your perceived probability of winning, then subtract 1. Formally, for outcome i that has odds of qi and a perceived probability of pi, the expected return for backing it is (qi * pi) – 1. Consider again the football fixture discussed earlier. The expected returns are as follows:
| Outcome | Bookmaker Odds | Your Perceived Probability | Expected Return Calculation | Expected Return |
|---|---|---|---|---|
| Manchester City Win | 1.36 | 60% | (1.36 * 0.60) – 1 | -18.4% |
| Draw | 4.75 | 25% | (4.75 * 0.25) – 1 | 18.8% |
| Stoke City Win | 9.00 | 15% | (9.00 * 0.15) – 1 | 35.0% |
| Totals: |
100%
|
|||
In this example you would choose to bet on both a draw and a Stoke City win.
It immediately becomes apparent that expected return is superior to the implied probability methodology, because the scale of value is easily observed. In the example above, both the draw and Stoke City are good value bets, but Stoke City is the best value. This has implications for how much of your account balance to wager on each outcome. Intuitively, the greater the value, the more you should wager. Formal betting strategies and the Kelly Criterion will be discussed in Sections 10 and 11 of this guide.
In the preceding analysis it was assumed that only two betting outcomes are possible. Either your bet wins and you receive a payout based on the odds, or it loses and you lose your entire wager. There are, however, bets where refunds or half payouts are possible. In these scenarios the expected return can be calculated as follows:
Expected return when a refund is possible
The best example of this scenario is a ‘draw no bet’ wager on a football game. For a fixture between Arsenal and Chelsea, if you place a ‘draw no bet’ wager on Arsenal, the bet wins if Arsenal wins, loses if Chelsea wins, and is refunded in the event of a draw.
When a refund is possible the expected return for outcome i is calculated as follows:
(odds on outcome i) * (probability of outcome i) + (1.00 * probability of draw) – 1
Note that the 1.00 is only shown for illustrative purposes, because a refund equates to a payout where the odds are 1.00. You can rewrite the equation as:
(odds on outcome i) * (probability of outcome i) + (probability of draw) – 1
Suppose the head to head odds are as follows, with your perceived probabilities of each outcome in brackets.
Arsenal win – 2.00 (40%)
Draw – 3.40 (20%)
Chelsea win – 3.80 (40%)
Now suppose the ‘draw no bet’ odds are:
Arsenal – 1.40
Chelsea – 2.75
Because a refund is possible the expected returns for backing each team are:
Arsenal: 1.4*0.4 + 0.20 – 1 = -24%
Chelsea: 2.75*0.4 + 0.20 – 1 = 30%
Based on these probabilities you would be inclined to back Chelsea in a ‘draw no bet’ wager. Note, however, that in the head to head market your expected return for backing Chelsea is 3.80*0.4 -1 = 52%. A head to head bet is better value, which means you are better off backing Chelsea in the head to head market than in a ‘draw no bet’ market. This is because you only placed a low 20% probability on a draw. Hence, you did not value the insurance aspect of a draw highly enough to take the lower odds in the ‘draw no bet’ market.
This result highlights the value of calculating expected returns. It enables you to select wagers from a number of markets on the same event.
Expected return when a half payout is possible
If a cricket fixture is called off due to bad weather, some bookmakers issue half payouts to all punters, rather than issue refunds.
When a half payout is possible the expected return on outcome i is calculated as follows:
(odds on outcome i) * (probability of outcome i) + 0.5 * (odds on outcome i) * (probability of a half payout) – 1
Suppose the odds on Australia and England in a one-day fixture are as follows, with your perceived probability of occurrence for each outcome in brackets:
Australia: 1.50 (50%)
England: 2.50 (40%)
Abandonment due to rain: half-payout (10%)
In the event of a half payout, Australia backers would get 1.50/2 = 0.75 odds, thus incurring a loss, while England backers would get 2.50/2 = 1.25 odds.
Your expected returns for backing each team are:
Australia: (1.50 * 0.50) + (0.5 * 1.50 * 0.10) – 1 = -17.5%
England: (2.50 * 0.40) + (0.5 * 2.50 * 0.10) – 1= 12.5%
Interestingly, if there is not a cloud in the sky and you have the same relative probabilities for each team winning, the expected returns become:
Australia: (1.50 * 0.5555) – 1 = -16.7%
England: (2.50 * 0.4444) – 1= 11.1%
The possibility of a half payout has increased the value of backing the underdog and lowered the value of backing the favourite.
Caveats
While the above discussion holds true in theory, in reality, your betting decisions are only as good as your perceived probabilities. The saying “garbage in, garbage out” applies here. If your perceived probabilities are inaccurate you will end up making poor decisions. This section provided a standardised way of assessing bookmaker odds, but the emphasis will always be on deriving accurate probabilities to apply in these models.
Notes and Sources
|
<< Previous topic: Tote (Parimutuel) vs. Fixed Odds Betting |
Next topic: Sports Betting Terms >> |

